ポートフォリオのリスクとは標準偏差(σ)のことでした。
なので、ポートフォリオの標準偏差(σ)を計算することで「リスク」を求めることができます。
その前提として、資産クラスAの標準偏差を「σa」、ポートフォリオにおける割合を「Wa」とし、その他の資産クラスについても同様とします。
また、資産クラスAと資産クラスBの相関係数を「Cab」とし、その他の相関係数についても同様とします。
このとき、資産クラスAと資産クラスBの2つから成るポートフォリオPの標準偏差「σp」は下記の計算式を解いて求めることができます。
- (σp)*(σp)=(σa)*(σa)*(Wa)*(Wa)+(σb)*(σb)*(Wb)*(Wb)+2*(Cab)*(σa)*(σb)*(Wa)*(Wb)
同様に、ポートフォリオPに資産クラスCを加えた場合の標準偏差「σp」は下記のとおりです。
- (σp)*(σp)=(σa)*(σa)*(Wa)*(Wa)+(σb)*(σb)*(Wb)*(Wb)+(σc)*(σc)*(Wc)*(Wc)+2*(Cab)*(σa)*(σb)*(Wa)*(Wb)+2*(Cac)*(σa)*(σc)*(Wa)*(Wc)+2*(Cbc)*(σb)*(σc)*(Wb)*(Wc)
なので、この要領でそれぞれの値を代入していくことでポートフォリオPのσ(リスク)を求めることができますよね。
以下、Excelを使って計算をしてみたのでメモしておきます。
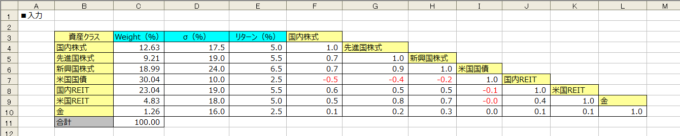
入力する値
こんな感じでExcelの表を作成しました。
資産クラス
資産クラスについては、通常は「国内・先進国・新興国」×「株式・債券・リート」の計9項目をよく目にしますが、今回は実践を重んじて、国内株式・先進国株式・新興国株式・米国国債・国内REIT・米国REIT・金の計7項目にしました。
債券については、社債を捨てて国債に絞りました。株式が暴落したときに社債は連れ安になりますが国債はむしろ上昇する傾向がありますよね。同じ債券でも、株式との相関係数は社債は正(プラス)ですが国債は負(マイナス)なので。
国債のうち、日本国債は個人投資家が購入しにくく、新興国国債は過去にデフォルト事例が多くあるので除外し、結果として米国国債のみを対象としました。
新興国REITに関しては、法整備を含めて投資環境が不安なので除外しています。
金(Gold)については、お金(法定通貨)よりも安定性が高く、史上最強の「価値保存の手段」だと思うので資産クラスに付け加えました。
Weight(重み付け)
ポートフォリオを構成する資産クラスの割合で、仮の数字をベタ打ちしています。
もちろん、合計すれば100%になります。
「σ(%)」と「リターン%」
各社が公開している情報を元にして鉛筆を舐めながら出した数字をベタ打ちしています。
相関係数
セルの【F3】から【L10】までが相関係数ですね。
これもネットで公開されている情報を元に自分でアレンジした数字をベタ打ちしています。
※相関係数については下記もご参照ください。
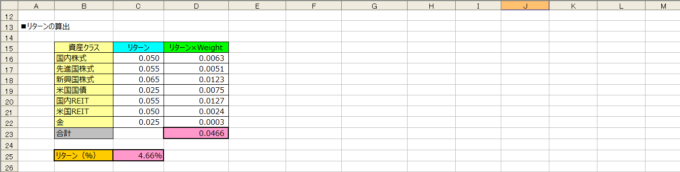
リターンの算出
こんな感じでExcelの表を作成しました。
リターンは「加重平均」というやつで簡単に計算できますよね。
求めるリターンはセル【C25】になります。
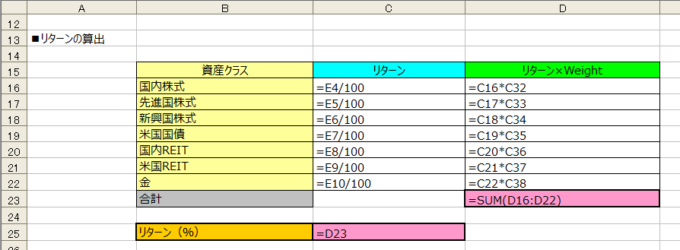
念のため、数式は下記のとおりです。
リスクの算出
ポートフォリオのリスク(σp)は下記の式を解けば求められましたよね。
- (σp)*(σp)=(σa)*(σa)*(Wa)*(Wa)+(σb)*(σb)*(Wb)*(Wb)+…+2*{(Cab)*(σa)*(σb)*(Wa)*(Wb)+(Cac)*(σa)*(σc)*(Wa)*(Wc)+…}
分かりやすくするために、前半部分(緑色)と後半部分(赤色)に別けて計算をしたいと思います。
- (σp)*(σp)=(σa)*(σa)*(Wa)*(Wa)+(σb)*(σb)*(Wb)*(Wb)+…+2*{(Cab)*(σa)*(σb)*(Wa)*(Wb)+(Cac)*(σa)*(σc)*(Wa)*(Wc)+…}
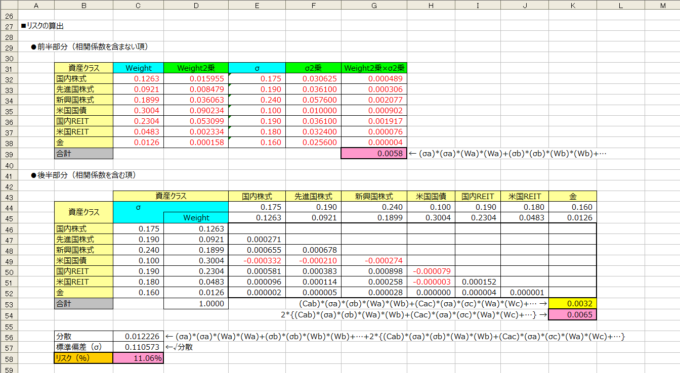
ちなみに、Excelの表はこんな感じです。
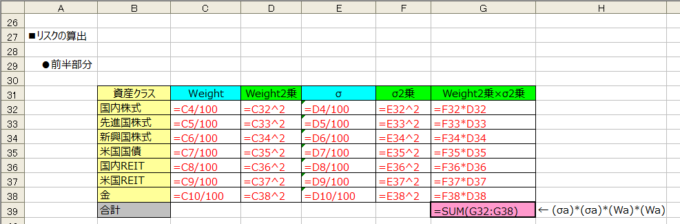
前半部分(相関係数を含まない項)
たとえば「国内株式」であれば、
- (σa)*(σa)*(Wa)*(Wa)
が、
- (国内株式のσ)*(国内株式のσ)*(国内株式のWeight)*(国内株式のWeight)
となり、同じ計算を資産クラスごとに算出して合算すれば前半部分は求められますよね。
求める値はセル【G39】になります。
念のため、数式は下記のとおりです。
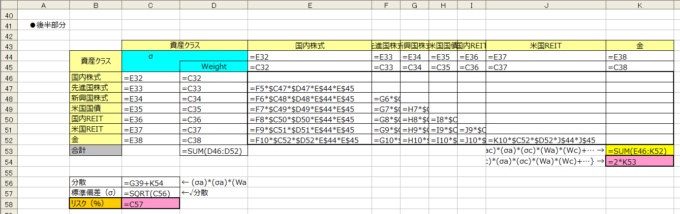
後半部分(相関係数を含む項)
ここが一番脂っこい部分ですよね。
教科書などを参照するとMMULT関数などを使ってスマートに計算していますが、自分が使い慣れていない関数は避けたいので、見た目はショボくても愚直に計算しました(そちらの方が理解しやすいと思いますし)。
まず、たとえば「国内株式」と「先進国株式」であれば、
- (Cab)*(σa)*(σb)*(Wa)*(Wb)
が、
- (国内株式と先進国株式の相関係数)*(国内株式のσ)*(先進国株式のσ)*(国内株式のWeight)*(先進国株式のWeight)
となり、これを求めるとセル【E47】になります。
同様の計算を資産クラスの対(ペア)ごとに算出して合算した値がセル【K53】になります。
ただし、後半部分の値はこの2倍なので、結局、セル【K54】が後半部分の値になります。
念のため、数式は下記のとおりです。
標準偏差(σ)
前半部分と後半部分を合算した値はセル【C56】になります。
でも、これって標準偏差ではなくて分散の値ですよね。
ご存知のように、求める標準偏差(σ)は分散の平方根なので、結局、このポートフォリオのリスク(σ)はセル【C58】の値になります。
おわりに
ポートフォリオの「リスク」をExcelで計算する方法をネットで探してみましたが、自分の好みに合ったシンプルなものがなかったので、自分で作ってみました。
【2018年10月03日追記】
ログを眺めていて、多くの方がアクセスしていることに気づきました。ありがとうございます。わざわざ手作業でExcelファイルを復元されるのもお手間だと思うのでファイルをダウンロードできるようにしました。個人の非商用に限りご自由にご利用ください(再配布は不可)。なお、本ファイルに関する一切の責任を負わないので予めご了承ください。
※2018年10月19日に一部修正(以前のバージョンでも計算そのものは問題ありません)。
確かめ算をして確認しているので多分大丈夫だと思うのですが、何か間違ってたらスミマセン。
【2018年12月07日追記】
効率的フロンティア曲線の作成手順を補足する記事を追加しました(機能追加バージョンのダウンロードも可能です)。