前回、MS-Excelを使ってポートフォリオのリスクとリターンを計算するスプレッドシートを作ったので、これを使ってシミュレーション分析をしてみたいと思います。
また、「3つ以上の資産クラスで構成されるポートフォリオの効率的フロンティア曲線の作図方法」についての補足もご参照ください。
株式投資のポートフォリオ
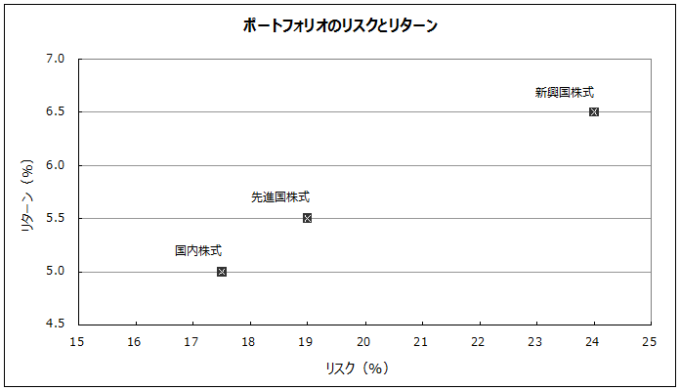
とりあえず、「国内株式」「先進国株式」「新興国株式」の3つの資産クラスを考えてみましょう。
これらを図表にプロットすると下記のようになります。
国内株式と先進国株式
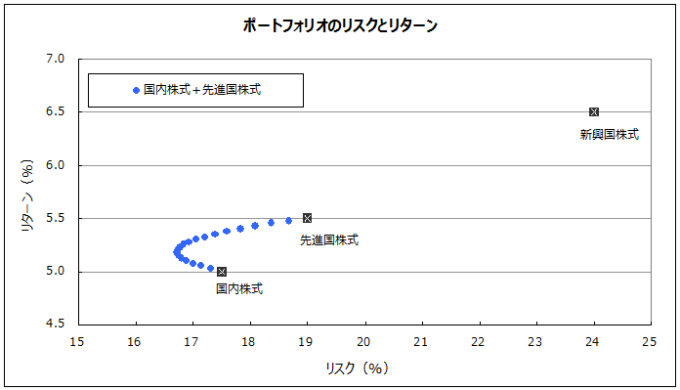
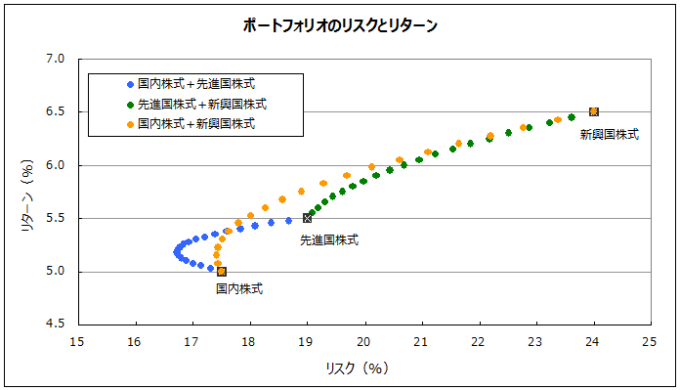
このうち、「国内株式」と「先進国株式」の2つの資産クラスから成るポートフォリオがあるとして、その組み合わせ比率を5%ずつ変化させると下記のようになります。
リスクは小さければ小さいほど、リターンは大きければ大きいほど好ましいので、この図表の中では左上であればあるほど好ましいことになりますよね。
そうすると、「国内株式」から左上に向かって伸びている「青い●」の幾つかは、「国内株式」よりも明らかにリスクは小さくてリターンは大きいことが分かります。
素晴らしいですよね。
たとえば具体的に、国内株式を40%、先進国株式を60%組み入れたポートフォリオは、
- ポートフォリオ:リスク17.0%・リターン5.3%
のようになり、国内株式
- 国内株式:リスク17.5%・リターン5.0%
よりも低リスクなのに高リターンとなります。
ちなみに、このような曲線のことを「効率的フロンティア」曲線と呼びます(正確に言うと曲線の下側は投資家が選好しないので上側のみです。さらにトービンの分離定理を使うと接点ポートフォリオが一意に決まり、無リスク資産と結んだ直線が効率的フロンティアになります)。
投資家が選択可能なポートフォリオの資産配分のうち、投資家にとって最も有利と考えられる選択肢の集合。同じリターンではリスクが最小に、同じリスクではリターンが最大になるような組み合わせを結んだ線上で表現される。
(野村證券)
英語でいうと「efficient frontier」ですね。
「efficient」は「無駄がなく効率的」で「frontier」は「最前線」という意味です。図表の左上が投資家にとってもっとも好ましい(無駄がなく効率的な)方向なので、つまり、その左上に向かった最前線という感じでしょうか。
国内株式と新興国株式
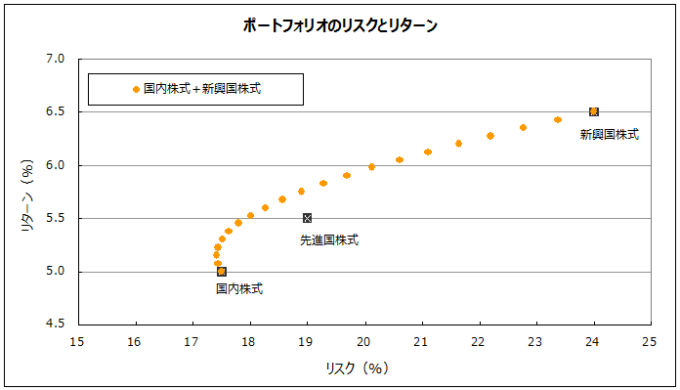
同様に「国内国株式」と「新興国株式」を組み合わせたポートフォリオは下図のとおりです。
これもいい感じですね。
先進国株式と新興国株式
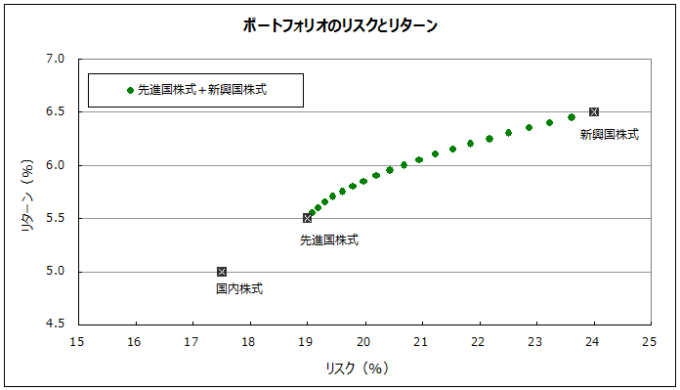
同様に「先進国株式」と「新興国株式」を組み合わせたポートフォリオは下図のとおりです。
これは両者を結んだ直線よりもわずかに左上の曲線になりますが、ポートフォリオの効果はイマイチ分かりませんね。
おそらく、両者の相関係数が「0.85」と大きいことが理由かもしれません。
国内株式と先進国株式と新興国株式
上記の3つのグラフを1つに合わせるとこんな感じです。
もちろん、これは2つの資産クラスから成るポートフォリオを図示しただけで、3つの資産クラスから成るポートフォリオとは異なります。
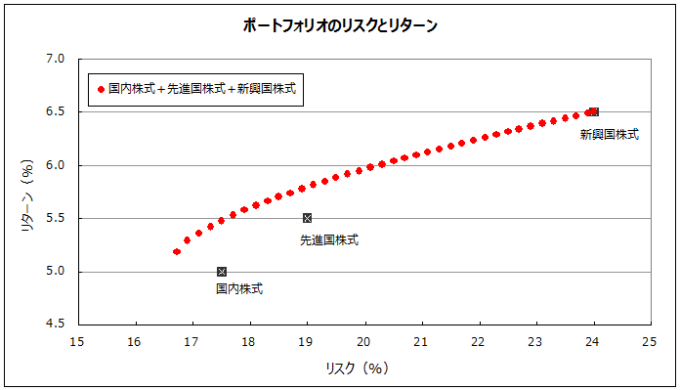
そこで、「国内株式」「先進国株式」「新興国株式」の3つの資産クラスで構成されているポートフォリオを作成し、Excelのアドイン機能である「ソルバー」を使って株式投資の効率的フロンティアを曲線を作成してみました。
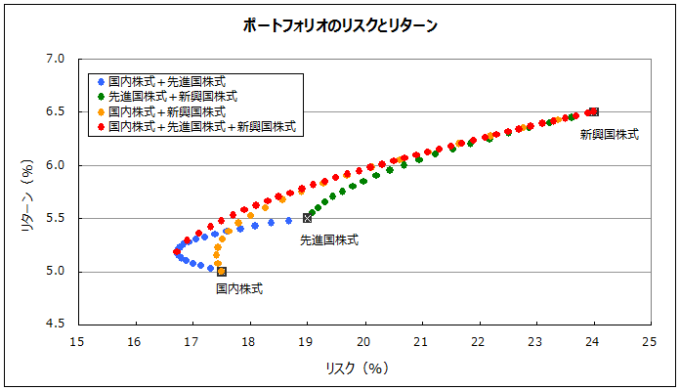
これを先の図表に重ね合わせると下記のとおりです。
2つの資産クラスを組み合わせた効率的フロンティア曲線上のどの点(青い●・緑の●・オレンジの●)よりも、「国内株式+先進国株式+新興国株式」を組み合わせた効率的フロンティア曲線(赤い●)が常に左上にある(つまり優れている)ことが分かりますよね。
株式投資をするなら、この効率的フロンティア曲線上のいずれかの点を選ぶのが経済合理的だということになります(どの点になるかは個人投資家それぞれの効用無差別曲線の形に依存します)。
もちろん、その点を選べば「どの資産クラスを何割組み入れるか」ということも決まりますが、問題は「どうやってその点を決めるか?」ということですよね。
(続きます)